AA Trees
If there's one thing I can take away from this project, it's that Wikipedia is a great resource for lists of things and an absolutely miserable experience for actually learning about them. Trying to read the descriptions for most of the tree structures on Wikipedia is like attempting to decipher ancient Greek. And this is a shame, because trees--even special trees like Red-Black or AA trees--are really not that complicated.
It's no exaggeration to say that we are surrounded by data trees. HTML is a tree--elements contained in other elements, all the way up to the <html> node. Levels in Doom were a special kind of tree called a Binary Space Partition. Your hard drive, of course, is a tree of nested directories. But even outside of computer science, trees are often a natural conceptual framework for expressing certain kinds of collective relationships: the Dewey Decimal System, for example, or a business's org chart, or (near and dear to my heart) the sections and sub-sections of a piece of legislation.
So if we were implementing a very simple tree, one with no optimization whatsoever, it would be pretty easy. In fact, it's not far off from our linked list, but instead of each item containing a single reference to a descendent, it contains a collection of references to zero or more children, and (optionally) a single reference up to its parent.
For applications where semantic meaning is more important than raw speed, the number of children per node is pretty arbitrary. On your hard drive, for example, you probably have some folders that are many levels deep, and some that are very shallow but contain a lot of objects, because the priority is to organize them logically so that you and your programs can find them. But if you're building a tree for doing searches or sorting behind the scenes, you want the "branches" of your tree to be all the same length and spread pretty much evenly around the structure, so that navigating around the tree and down each branch takes a consistent amount of time.
In this post we're going to build one of these search-optimized trees--a so-called "self-balancing binary search tree." And the difference between those and a regular, ad-hoc tree is simply the addition of three constraints:
- It has a maximum of two children per node (usually called left and right)
- It has a set of rules for determining when a branch is too deep or too wide after insertion or deletion, and
- It has a clearly-defined procedure for rearranging the tree when the rules are violated to bring it back into compliance.
To navigate a tree built this way, you take your search value, and you compare it to the node at the root (which is traditionally at the top: binary trees grow down. Imagine they're in Australia, if that helps). If it's bigger than the value assigned to the root, you move to the child on the right side. If it's smaller, you move to the left. Then you do the comparison again, until you either hit the value you want, or you hit the end of the tree (where you may insert the value so you can find it next time). Here's an example of a node from one of these trees, followed by an algorithm for traversal.
var node = {
left: null, //reference to left-hand child (usually lesser)
right: null, //reference to right-hand child (usually greater)
key: 0, //the node key, used for lookup
data: null //the actual value of the node
}
//walk() recursively traverses a tree made of these nodes
//Then it renders it out visually to the console
function walk(tree, depth, side) { //depth and side are used for internal record-keeping
if (!depth) depth = 0;
if (!side) side = "";
var padding = "";
for (var i = 0; i < depth; i++) padding += "| "; //add spacing to the output
console.log(padding, side, tree.key, tree.data); //display the tree
//now we walk down the branches, if they exist
if (tree.left) walk(tree.left, depth + 1, 'left');
if (tree.right) walk(tree.right, depth + 1, 'right');
}
Recursion--creating functions that call themselves--is an essential strategy for being able to use trees, so if you're not very good with it, now would be a good time to study up.
Today we're going to implement an AA tree, which is named for its inventor, Arne Andersson (original paper available here), not for the support group ("Hi, I'm Thomas, and I'm a data structure." "Hi, Thomas!"). I picked the AA tree from all of the binary search trees because its rules for maintaining balance are extremely simple, and I didn't particularly want to spend a long time working through edge cases and chasing bugs. An AA tree is built by adding a level value to each node, and then following these five rules:
- Leaf nodes (the null values that terminate each branch) are at level one.
- Left children have to have a level value less than their parent.
- Right children must have a level less than or equal to their parent.
- Right grandchildren, however, must have a level less than their grandparent.
- Any node with a level higher than one has to have two children.
A skew is used to fix a violation of rule two, where the left child is at the same "level" as its parent. It rotates the tree so that the left child becomes the new parent, with the old parent as its right node and its old right node moved underneath. For once, Wikipedia's illustrations are actually pretty good:
 And here's the code for skew():
And here's the code for skew():
function skew (branch) {
if (!branch || !branch.left) return branch; //basic input validation
if (branch.left.level >= branch.level) {
var swap = branch.left;
branch.left = swap.right;
swap.right = branch;
return swap;
}
return branch;
}
A split fixes violations of rule 4, where the rightmost grandchild of a node (so the right reference of its right reference) has the same level value. It makes the right child the new parent node, with its parent as the new left reference and its former left child takes its place as the right child node on the old parent. Again, from Wikipedia:
 Here's our split() code:
Here's our split() code:
function split(branch) {
//basic input validation
if (!branch || !branch.right || !branch.right.right) return branch;
if (branch.right.right.level >= branch.level) {
var swap = branch.right;
branch.right = swap.left;
swap.left = branch;
swap.level++;
return swap;
}
return branch;
}
It may help, when trying to figure out exactly what these functions are doing, to remember that a binary search tree is basically a number-line with a bunch of connections starting from an arbitrary middle node somewhere. Or, to put it another, way, if you squash a tree down onto a single "level", you get the following:
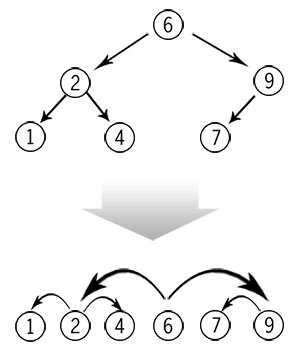 So all of these operations--skew, split, insertion, and deletion--are ways of changing the links between nodes without altering their horizontal order. The tree above, for example, could easily have 4 as its head node, linking from there to 2 and 7 (and from those to 1 and to 6 and 9, respectively), but the order of the nodes when flattened remains the same, and the same rules of traversal (go left if less, right if greater) still apply. This would make a pretty decent Professor Layton puzzle, actually.
So all of these operations--skew, split, insertion, and deletion--are ways of changing the links between nodes without altering their horizontal order. The tree above, for example, could easily have 4 as its head node, linking from there to 2 and 7 (and from those to 1 and to 6 and 9, respectively), but the order of the nodes when flattened remains the same, and the same rules of traversal (go left if less, right if greater) still apply. This would make a pretty decent Professor Layton puzzle, actually.
Enough theory, let's start adding values. Whenever you do an insertion on the tree (deletions are more complicated), you start by traversing the structure to see if the value exists. If it doesn't, you add it at the end of a branch with a level of 1. Then work your way back up to the root on the back half of the recursion, rebalancing as you go with a skew and a split. You skew first, because the reverse makes it possible to end up in an invalid state and you'd have to perform the balancing operations all over again.
insert: function(key, data, branch) {
if (branch.key == key) {
branch.data = data;
return branch; //If we find a match for the key, just update in place
}
if (key < branch.key) {
if (branch.left) {
branch.left = insert(key, data, branch.left); //recurse to the left
} else {
branch.left = new AANode(key, data); //at the leaf, add the new node.
}
} else {
if (branch.right) {
branch.right = insert(key, data, branch.right); //recurse to the right
} else {
branch.right = new AANode(key, data); //at the leaf, add the new node.
}
}
branch = skew(branch);
branch = split(branch);
return branch;
}
Deletions, as I said, are more complicated, but they're not terribly hard to understand--the deletion part, at least. Once again, we walk the tree to find the value, but this time we hold onto it for a little bit while we go looking for its nearest key to swap into its place. We find that by walking down either the left or right branch (either will do) one step, then going the other direction until we reach a null (i.e., for the precursor value, we walk left once, and then repeatedly right). We swap the replacement node's data and key with those of the node to be deleted, and then prune the end of the branch.
remove: function(key, branch) {
if (!branch) return branch; //if we recurse past the end of the tree, return the null value.
if (key < branch.key) {
branch.left = remove(key, branch.left);
} else if (key > branch.key) {
branch.right = remove(key, branch.right);
} else {
//if this is a leaf node, we can just return "null" to the recursive assignment to remove it.
if (!branch.left && !branch.right) return null;
//we look for the "closest" key in value, located at the end of one of the child branches
var parent = branch;
if (branch.left) {
var replacement = branch.left;
while (replacement.right) {
parent = replacement;
replacement = replacement.right;
}
} else if (branch.right) {
var replacement = branch.right;
while (replacement.left) {
parent = replacement;
replacement = replacement.left;
}
}
//we swap the replacement key and data into the to-be-removed node
branch.key = replacement.key;
branch.data = replacement.data;
//then remove the replacement node from the tree, thus completing the "swap"
//we can't do this in the while loop above, because technically it could
//be either child, regardless of initial search direction.
if (parent.left == replacement) {
parent.left = null;
} else {
parent.right = null;
}
}
//decrease levels, in case they've gotten out of control
var minLevel = branch.left ? branch.left.level : branch.level;
minLevel = branch.right && branch.right.level + 1 < minLevel ?
branch.right.level + 1 :
minLevel;
if (minLevel < branch.level) {
branch.level = minLevel;
if (branch.right && minLevel < branch.right.level)
branch.right.level = minLevel;
}
//rebalance, using the sequence given in Andersson's paper.
branch = skew(branch);
branch.right = skew(branch.right);
if (branch.right) branch.right.right = skew(branch.right.right);
branch = split(branch);
branch.right = split(branch.right);
return branch;
}
It looks complicated, but it's really not that bad. The most confusing part is probably the swap in the middle, but if you remember the number-line version of the tree, all we're doing is switching the to-be-deleted node's position in the tree with it's neighbor, so the rules of left and right traversal remain valid. Then, because the neighbor was at the bottom of its branch, we can drop the now-swapped node from the tree without worrying about its children. The most conceptually-difficult part of the delete operation is the rebalancing at the end, but Andersson's paper provides a sequence of splits and skews that we can simply follow in order.
Implementing these trees in JavaScript was a challenge, not because they're hard, but because of a language quirk: JavaScript is strictly pass-by-value, except where the argument being passed in is an object, in which case what gets passed in is a reference to the object, still passed by value. In this, it's basically like Java. As a result, you can alter properties of the object because you have a reference to it, but you can't replace it or modify it wholesale, because that changes the value of the reference to something completely new, while leaving the old reference unchanged in the caller's scope. You can't, in other words, write a swap(a, b) function in JavaScript, which is a shame, since (you may have noticed) maintaining these trees requires a lot of swaps.
I started out trying to write my skew and split functions with reassignments done in the function scope, just as in Andersson's paper (which is written in Pascal-like syntax, and Pascal is a pass-by-reference language). But when the function exited, my node arrangements would be unchanged--or worse, would be altered in bizarre and unpredictable ways--because I was unknowingly operating on and assigning new references that only existed in the local scope. Changing my functions to expressly use return values eliminated the problem. It also made my code more verbose and difficult to read, in my opinion. But once I came to grips with correct JavaScript calling style, the rest fell into place pretty quickly. Deletion was the hardest part: I eventually went back to the original paper, re-read the prose description, and implemented a "clean room" version of it.
Maybe because you're not actually supposed to touch the inside of a tree as much as you do a list, this actually ended up being much simpler than the linked list from last post. There's more theory, but arguably less bookkeeping. As before, I wrote it as a functional library object, then wrapped it up in an object that maintains the references to the structure in working order. I like it, and could definitely see myself using these for something in JavaScript--as you're about to see.
Demonstration
This time, I want to demonstrate using this structure for a real purpose, not just a get/set interface. So here's what we're going to do: when you click the Start button below, a script will pull in the contents of this post and store each word and its frequency in an AA tree structure. Don't worry, it's surprisingly quick. At that point, you can start typing into the text box below. As you do, it'll search through the tree with the closest option (which returns the last non-null branch it finds) to autocomplete a word (shown in the "do you mean..." link). If it finds an exact match, or if you click the link to use the auto-completion, it'll tell you how many times I used that word. The tree structure should be fast enough to do autocompletion in realtime, which is pretty cool.
As always, the code for the example is here, and the underlying tree implementation is here, both with as many comments as my poor eyes could stand. If you're the adventuresome type, you can access the actual tree structure from your console via window.demos.aaTreeDemo (I recommend calling window.demos.aaTreeDemo.tree.render(), if you're curious about the resulting structure). Once you've prepped the tree, you can also see a simple ASCII-style rendering of its structure (with the direction, key, data, and level of each node) using the View Tree button, but be warned: it's long.